Teaching maths to include procedural variation is central to the current debate around teaching with a mastery approach. So what does procedural variation mean and how will it change your primary maths teaching?
I prefer ‘teaching with variation’ to the term ‘intelligent practice’ which is also used, as this implies that any alternative practice is unintelligent. However, whichever term is used, they are both methods for providing repetitive learning, or practice, with more likelihood of a positive impact on understanding than random practice exercises or rote learning.
When presented in practice exercises they may appear repetitive, but it aims to highlight the essential features of the concepts to the children through varying the non-essential features. The fewer the number of differences and the clearer the aspect that changes, the more chance that the children will focus their attention on that intended concept.
As I have mentioned a number of times in articles on mastery, there is very little that is completely new but this is a welcome change in emphasis and should be helpful to teachers in developing a systematic and considered approach to teaching maths concepts, procedures and skills.
Variation theory came to attention from studies of teaching approaches in China, which linked to John Mason and Anne Watson’s work ten years ago on teaching for conceptual understanding and using variation to structure sense-making.
Variation theory came to attention from studies of teaching approaches in China, which linked to John Mason and Anne Watson’s work ten years ago on teaching for conceptual understanding and using variation to structure sense-making.
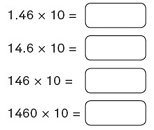
1. Extending a problem by varying the number, the unknown or the context
When you ask your class the question, ‘use what you know to work out what you don’t know’ this is similar to this type of variation. They are often a short bank of questions that build up from a simple start and practice the aspect you want to focus on. For example, varying the number but using number facts or place value, see above right, with 6+9 and 7x4.
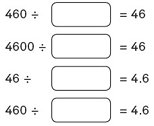
Here are two more examples that show variation, varying the number and then the unknown:
2. Varying the processes of solving a problem
I think we’re pretty good at this – the Numeracy Strategy emphasised it and I observe a lot of teachers that use a number of different processes to solve a problem. The question ‘How did you work it out?’ opens up so many opportunities to explore the process the children go through to get to the answer, picking up misconceptions or errors and giving you the chance to deepen children’s understanding by breaking down those processes and applying them to other problems.
As well as the processes for solving a problem it could also focus on the procedures a child uses. For example, for subtracting money when giving change, children could explore taking away, they could line the coins up as they add and they could show their counting on through jumps on a number line. Use the same numbers and vary the method or process. At the end ask, ‘What is the same and what is different?’ and ‘Which method did you prefer?’
I think we’re pretty good at this – the Numeracy Strategy emphasised it and I observe a lot of teachers that use a number of different processes to solve a problem. The question ‘How did you work it out?’ opens up so many opportunities to explore the process the children go through to get to the answer, picking up misconceptions or errors and giving you the chance to deepen children’s understanding by breaking down those processes and applying them to other problems.
As well as the processes for solving a problem it could also focus on the procedures a child uses. For example, for subtracting money when giving change, children could explore taking away, they could line the coins up as they add and they could show their counting on through jumps on a number line. Use the same numbers and vary the method or process. At the end ask, ‘What is the same and what is different?’ and ‘Which method did you prefer?’
3. Varying the problems by applying the same method to a group of similar problems
This, again, I see used frequently in our classrooms. This is the classic modelling and scaffolding approach so that a strategy or procedure is taught and then used to solve different problems. For example, if a class has learnt all about multiples and lowest common multiples they could apply this understanding when learning how to compare fractions and search for common denominators.
This also shows the connections between all the areas of mathematics and how skills and concepts can be used and applied in many different contexts.
This, again, I see used frequently in our classrooms. This is the classic modelling and scaffolding approach so that a strategy or procedure is taught and then used to solve different problems. For example, if a class has learnt all about multiples and lowest common multiples they could apply this understanding when learning how to compare fractions and search for common denominators.
This also shows the connections between all the areas of mathematics and how skills and concepts can be used and applied in many different contexts.
So these types of questions are not new, I’ve found examples in books that I wrote back in 1997 and most books since, however it was perhaps not presented in the same very systematic way.
It is the first type of prodecural variation, Extending a problem by varying the number, the unknown or the content, that perhaps has not had enough emphasis in our classrooms. Much of the practice in books or worksheets tends to be more random so the child has to think carefully about each question. There is a place for this type of practice too, certainly at the end of the teaching to check that children have learned and understand the procedure or concept. Developing questions that involve variation does require some careful thought but they certainly help make the ‘practice’ part of a lesson a valuable part of the learning process.
It is the first type of prodecural variation, Extending a problem by varying the number, the unknown or the content, that perhaps has not had enough emphasis in our classrooms. Much of the practice in books or worksheets tends to be more random so the child has to think carefully about each question. There is a place for this type of practice too, certainly at the end of the teaching to check that children have learned and understand the procedure or concept. Developing questions that involve variation does require some careful thought but they certainly help make the ‘practice’ part of a lesson a valuable part of the learning process.