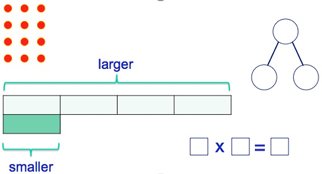
Following on from my earlier article on teaching maths with procedural variation, there is another type of variation used when teaching maths: conceptual variation. This time, instead of varying the problem, the problem stays the same and the representation of the problem is varied. This is generally through the use of models or images.
As shown here, a multiplication problem, say 3 x 4, could be represented in an array or using a bar model. The numbers within the problem could be arranged in a triangular arrangement or in a standard multiplication format. By keeping the question the same and showing it in different ways, the underlying structure of the operation (or whatever skill, concept or procedure is being learnt) can be explored and help the child make sense of the maths.
I have always liked Haylock and Cockburn’s assessment idea of checking a child’s understanding through this activity. It is a simple and effective example of conceptual variation.
Give a starting point for a problem, for example 6 + 3 = __
Provide children with :
• some cubes and counters
• a number line
• paper and a pencil
• a calculator
Your children then model the problem and show the answer using the number line, the cubes, on a calculator and through writing a word problem.
Give a starting point for a problem, for example 6 + 3 = __
Provide children with :
• some cubes and counters
• a number line
• paper and a pencil
• a calculator
Your children then model the problem and show the answer using the number line, the cubes, on a calculator and through writing a word problem.
Variation, both conceptual and procedural, is an important element of a mastery approach. However, variation is not new, I’ve found examples in books that I wrote back in 1997 and most books since, although it was perhaps not presented in the same very systematic way. These teaching approaches in China were linked to John Mason and Anne Watson’s work ten years ago on teaching for conceptual understanding.
It is useful to look again at our approach to teaching primary mathematics to see how our current practice can be developed and improved. If a child sees the same concept represented in a number of carefully planned ways it brings the focus of their attention to that important idea or concept. The variation of one aspect, with other aspects kept the same, helps children spot patterns, structures and relationships that could otherwise be lost in the complexities of the usual 'variety' in practice. Variety is still important, particularly when assessing understanding or using a skill or procedure in different contexts, but variation is particularly effective when it directly follows some focussed teaching.
It is useful to look again at our approach to teaching primary mathematics to see how our current practice can be developed and improved. If a child sees the same concept represented in a number of carefully planned ways it brings the focus of their attention to that important idea or concept. The variation of one aspect, with other aspects kept the same, helps children spot patterns, structures and relationships that could otherwise be lost in the complexities of the usual 'variety' in practice. Variety is still important, particularly when assessing understanding or using a skill or procedure in different contexts, but variation is particularly effective when it directly follows some focussed teaching.