I have chosen my Christmas cards for this year – with a maths theme, of course. The cards are from Cancer Research and have a design based on the Twelve Days of Christmas. This links to one of my favourite Christmas problems for your class to solve:
What I like about this problem is that all children can have a go; some can use models or pictures to build up the totals for each day, some children will use addition and not see any patterns – until perhaps they get a prompt from you!
For me a perfect investigation or problem is one that all children can dive into from a simple starting point, but that allows them to move on and become challenged through teacher prompts or through the child’s own questioning.
For me a perfect investigation or problem is one that all children can dive into from a simple starting point, but that allows them to move on and become challenged through teacher prompts or through the child’s own questioning.
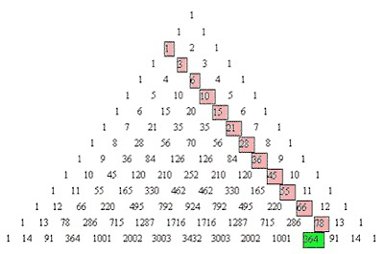
The total number of presents given each day are highlighted on this triangle and show 1 present on the first day, 3 on the second day and so on.
What is interesting is that the running totals, 1, 4, 10, 20… are in the row below, up to 364 presents altogether for the 12 days.
Just to be clear, by the end of the second day there are a total of 4 presents; 1 on the first day + 3 on the second day. By the end of the third day there are the 4 presents (from day 1 and 2) and another 6 presents (3 french hens, 2 turtle doves and a partridge in a pear tree) making a total of 10.
Matthew, a Y6 boy I taught a few years ago, devised his own triangle to solve the problem. He hadn’t come across Pascal’s Triangle and, amazingly, I haven’t seen numbers arranged like this before.
For each day he wrote the running totals for each present received in a row. So, for example, on day 3 the totals were 3 partridges, 4 turtle doves and 3 french hens. He continued this for each row and then spotted all the patterns of multiples. Brilliant.
Here is part of his investigation – has anyone used a version of ‘Matthew’s Triangle’ before?
For each day he wrote the running totals for each present received in a row. So, for example, on day 3 the totals were 3 partridges, 4 turtle doves and 3 french hens. He continued this for each row and then spotted all the patterns of multiples. Brilliant.
Here is part of his investigation – has anyone used a version of ‘Matthew’s Triangle’ before?
For Broadbent Maths users:
Download ready to use 12 Days of Christmas problem solving cards to start off this investigation.
Download ready to use 12 Days of Christmas problem solving cards to start off this investigation.
Related articles:
A song to start 12 Days of Christmas investigation
Hoopla Kidz has some good YouTube songs and it's 12 Days of Christmas is a nice start to this investigation
How many ways can a star be drawn?
Separate activities for KS1 and KS2 to explore this question.
Make a star for Christmas
Creative shape and measures activities - perimeter, angles and proprties of 2D shapes.
A song to start 12 Days of Christmas investigation
Hoopla Kidz has some good YouTube songs and it's 12 Days of Christmas is a nice start to this investigation
How many ways can a star be drawn?
Separate activities for KS1 and KS2 to explore this question.
Make a star for Christmas
Creative shape and measures activities - perimeter, angles and proprties of 2D shapes.