Functions

Give pupils experience of the following stages when looking at functions:
 
·     Function machine

 
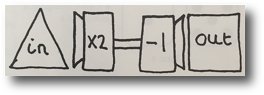
·     Table of results

 
·     Number pairs

(1, 1) (2, 3) (3, 5) (4, 7) (5, 9)

 
·     Graph

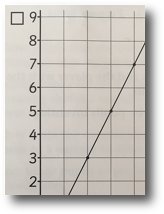
·     Function

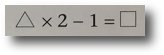
This can be developed by using letters instead of symbols.
 
 

Equations

Discuss with pupils the fact that any letter can replace any number.

Give problems that involve the use of letters instead of numbers in the answer:
 
If x cakes cost 24p, what does one cake cost?
 
Beads are put in sets of twelve. How many beads in dsets.
 
The sides of a square are y cm long. What is the area of the square?
 
An ice cream costs 45p. what is the cost of c ice creams?
 
Give the pupils an opportunity to make up their own problems.
 
 

What is the rule?

Make cards which show pairs of numbers with an arrow representing various possible rules to describe their relationship.

Discuss with the pupils what the arrow could represent:
 
One operation:          + 5            + 4                ÷ 2
Two operations:        x 2 + 1       x 2 + 1          + 3 ÷ 3

Conversion machines

Set up a box as a money function machine. Pupils use the function machine to convert pence into pounds. The conversion can be written on pieces of paper.

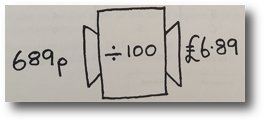
Extend this activity to converting centimetres to metres, grams to kilograms and millilitres to litres.
 
 

 

Function machine booklets

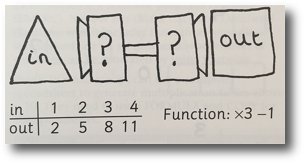
Groups of pupils design and draw their own function machines to make into a booklet. The machine should include clear IN and OUT sections and either a one- or two-stage function. They draw a table of results for others to work out the function.
 
 

Function challenges

Pupils draw tables of results and graphs for different functions:

And some tricky ones:

Matchstick sequences

Pupils use headless matchsticks to generation number patterns.

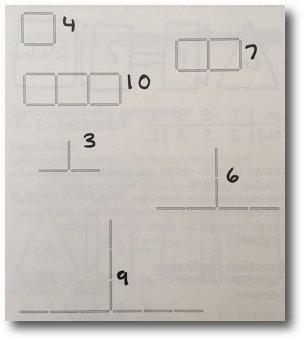
Encourage them to make a pattern that shows a sequence and not just a shape pattern.
 
When they have made a sequence they can glue it onto a card and write about the pattern.
 
They can use a table of results to help them work out a formula for the sequences:
 
S = Shape number
R = Number of matchsticks
 
 

 
     R = 3S + 1
 

Coordinates

Show pupils that the coordinates for a position are written as ordered pairs: (4, 7).
 
Pupils draw a simple shape on squared paper, ensuring that the vertices are where coordinates meet.
 
They write the coordinates for their shape and give them to a partner to draw. 

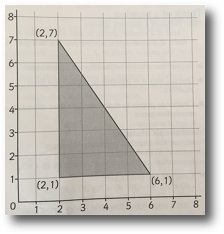
Encourage pupils to predict the shape from the coordinates.
 
To develop this, pupils multiply each of the coordinates by 2 and compare the areas of the enclosed shapes.
 
 

Square number patterns

Show pupils that to find the square of a number, you can multiply the numbers each side of it and add 1:
 
2²= (1 x 3) + 1
 
3²= (2 x 4) + 1
 
4²= (3 x 5) + 1
 
They investigate other square numbers to see if the pattern continues.
 
 

Cube number patterns

Pupils investigate the pattern for forming cube numbers.
 
2³= (1 x 2 x 3) + 2
 
3³= (2 x 3 x 4) + 3
 
4³= (3 x 4 x 5) + 4
 
They find other cube numbers and check their answers with a calculator.
 
 

Factors

The number 16 has the factors 1, 2, 4, 8, 16.
 
All the factors are even except for 1.
 
Pupils investigate other numbers that have only even factors, except for 1.
 
They should find that they are all powers of 2 (2, 4, 8, 16, …)
 
 
 

Venn and Carroll Diagrams

Arrange a labelled Venn or Carroll diagram on a table. Add labels such as: multiples of 6, triangular numbers, square numbers, odd and even numbers.

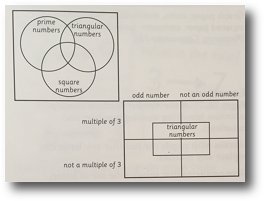
Pupils have the numbers 1-30 written on small pieces of paper to place on the diagram.
 
Extend the activity by allowing the pupils to rearrange and alter the labels and to use a greater range of numbers.
 
 

Factor trees

Pupils draw factor trees by splitting numbers into multiplication facts.

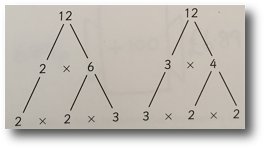
Discuss the patterns generated and the fact that the final ‘branches’ for a starting number will always be the same.


 

Dice total game

For this game four dice are needed. Each player takes turns to throw the dice and arrange them in two groups. They total each group and for each total they score one point if it is: even, prime, triangular, or a multiple of 3.

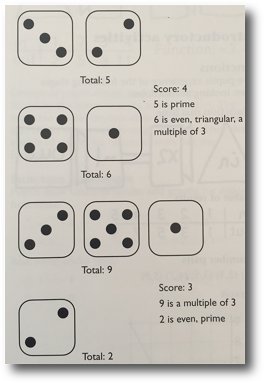
Each player has five throws and the player with the highest score at the end wins.
 
The game can be extended by pupils inventing their own rules.

Cube sequences

Pupils make sequences of interlocking cubes. Encourage them to explain how the pattern is growing. The number patterns can be shown in a chart.

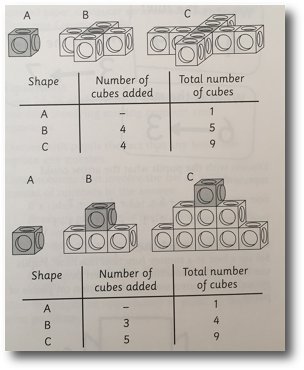
The Fibonacci sequence

In 1202 the Italian mathematician Leonardo Fibonacci wrote a book called Liber Abaciwhich included a problem about breeding rabbits. The solution is found by continuing the sequence of Fibonacci numbers:
 
1, 1, 2, 3, 5, 8, 13, 21, …
 
Pupils can investigate this sequence, continuing it and trying to find patterns and a rule for generating these numbers.
 
 

Growing rectangles

Pupils can find Fibonacci numbers by making growing rectangles:

These rectangles grow in the same sequence as the Fibonacci sequence.  

Encourage pupils to find out about the Golden rectangle and its link with Fibonacci numbers.