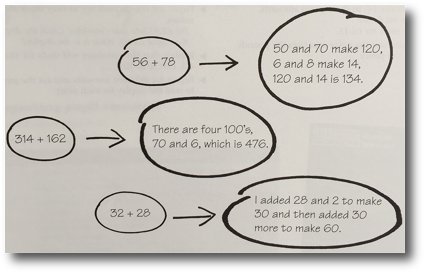
Mental calculations
· Practise adding and subtracting two-digit numbers where there is no exchange involved, such as 31 added to 53 and 37 subtract 15.
Discuss with pupils how they did this.
· Extend the addition to include exchange situations, such as 27 added to 35. Pupils may find it helpful to close their eyes and do it in two stages. For example:
Add the tens first (20 add 30). Put that answer of 50 in your memory like a calculator.
Add the ones (7 add 5), recall the memory number and add it to 12.
What is the answer?
· Discuss other ways in which pupils might do this.
· Ask pupils to double two-digit numbers.
· Put these mental activities in the context of money by asking them to total amounts.
Countdown
Choose seven random numbers between 1 and 40 and write them on the board.
Write a target number between 50 and 500.
The pupils use any of the numbers once only and any number operations to try to make the target number. A time limit of, say, three minutes may be given.
Mental addition
Pupils should be encouraged to describe their mental methods for adding 2- and 3-digit numbers and share them with others.
The ability to count up is a useful skill. Pupils may find it helpful to keep their eyes closed and to count up in stages:
Count up from 426 to 500.
Count up to 430 first. Put that number in your memory like a calculator.
Count up from 430 to 500. Recall the memory number.
What is the answer?
Also discuss compensation skills such as:
Add 9 → add 10, take away 1
Add 98 → add 100, take away 2
Add 47 → add 50, take away 3.
Doubles tennis
This is a game to practise the doubles of multiples of 10 up to 1000.
One pupil starts with any multiple of 10 up to 1000 and asks the other pupil for the double of that number. Once the answer is given, that pupil chooses a different number and continues to ‘rally’ with another child until a mistake is made, e.g.
Ali... Double 120?
240. Kate... Double 70?
140. Mark... Double 490?
Extend the numbers to 1000.
Modelling addition
Pupils use base 10 apparatus to model addition and to talk through and describe the operation.
· Ask pupils to put out 274 and 347. They add the numbers together.
Use a questioning approach to allow them to use appropriate language.
What shall we add first?
Where shall we put the tens?
How many hundreds have we?
What is the total of these two numbers?
Include addition of three and four numbers. These can generate carry figures other than 1.
· Discuss written algorithms for additions. Decide whether to show a carrying figure under the tens and hundreds columns or to ask the pupils to hold this figure in their heads. If your School Policy recommends a specific method for recording carrying figures, show that method.
Modelling decomposition
There are four different decomposition situations for subtraction of HTO. These are:
Exchanging a ten for ones: 373 – 149
Exchanging a hundred for tens: 546 – 384
Exchanging a ten for ones, then a hundred for tens: 726 – 489
Exchanging a hundred for ones: 402 – 125
Introduce each of these separately with pupils using base 10 apparatus to act out and describe the decomposition. Use a questioning approach to develop language appropriate to this method of subtraction.
· Exchanging a ten for ones
Ask pupils to put out 373.
Now ask them to take away 149 from 373.
How are you going to take away the nine ones?
What can you change to get extra ones?
· Exchanging a hundred for tens
Ask pupils to put out 546.
Now ask them to take away 384 from 546.
How are you going to take away the eight tens?
What can you change to get extra tens?
· Exchanging a ten for ones, then a hundred for tens
Ask pupils to put out 726.
Now ask them to take away 429 from 726.
How are you going to take away the nine ones?
How are you going to take away two tens?
· Exchanging a hundred for ones
Ask pupils to put out 402.
Now ask them to take away 125 from 402.
How are you going to take away the five ones?
What are you going to change as there are no tens?
Adding three-digit numbers
Discuss ways of adding three-digit numbers ‘in your head’ when no exchange is involved, such as 432 plus 345. Pupils may find it helpful to close their eyes and do this in stages:
Total the hundreds first and put the total in your memory, like a calculator.
Total the tens and add the total to the memory number.
Now total the units and add that to the memory number.
What is the total?
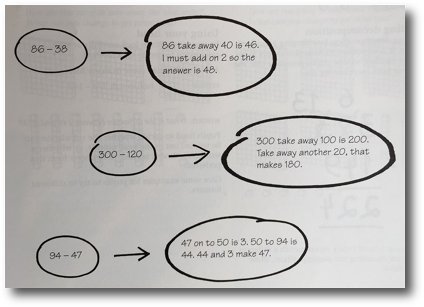
Mental calculations
Pupils describe their mental methods for subtraction and share them with others.
Discuss compensation skills such as:
Take away 9 → take away 10 add 1
Take away 97 → take away 100 add 3
Take away 48 → take away 50 add 2.
The ability to count up is a useful skill. Pupils may find it helpful to keep their eyes closed and to count up in stages:
Count up from 356 to 400.
Count up to 360 first. Put that number in your memory like a calculator.
Count up from 360 to 400. Recall the memory number.
What is the answer?
Limit the digits
Organisation: groups or individualsUsing the digits 1, 2, 3, 4, 5, 6, pupils make different additions.

What is the smallest?
What is the nearest to 500?
Dice game
· Pupils work in pairs with two dice and a 5 x 5 grid between them.
· They take turns to roll the two dice and decide whether to add or subtract the scores.
· They enter the answer anywhere on the grid.
· The aim is to make a line of numbers that totals 15 horizontally, vertically or diagonally.
Differences
Organisation: groups or individuals
Using a shuffled pack of Digit cards 0-9, pupils take the top 6 cards and arrange them to make a HTU – HTU subtraction with the smallest difference.
Dice crash
· Each player rolls a dice as many times as they wish, to obtain a total.
· Players can stop at any time and pass the dice to the next player.
· They add the total to their overall score. A crash occurs when a 1 is rolled.
· Rolling a 1 on the dice makes the total for that round zero.
· The first player to reach 100 wins the game.
· Players should check each others’ mental addition.
· A written record of the total for each round of the game would be helpful.
Four corner totals
Organisation: groups or individualsPupils draw a square and find four corner numbers which total the centre number.
Change the centre number.
Change the square to a pentagon.

Which are tricky additions? Why?
Make 999
Organisation: groups or individualsPupils find different combinations of two or three three-digit numbers which will total 999.
They record their results and look for patterns in the calculations.

Reverse add
Organisation: groups or individualsPupils make a three-digit number from digits 0 to 5, then reverse the three-digits to make another number. They add these. They repeat for other choices of digits and write a sentence to describe their results.

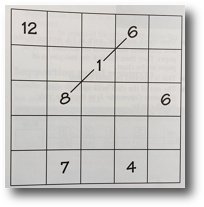
Use a set of digit cards 1-9.
· Place 4 in the centre of a 3x3 grid
· Place the other digits on the grid, making as many rows, columns and diagonals total fifteen as possible
· Use a systematic approach and record the answers to avoid repeating results
· Extend the problem by making the totals 16, 17, 18, ...

Add opposite corners (2 + 14) then find other rectangles on the hundred square whose opposite corners also have this total.
You may notice that both pairs of opposite corners always have the same total (2 + 14 = 12 + 4)
Explorte different totals and draw the different rectangles on squared paper.
Use a systematic approach such as having 1, 2, 3, 4, 5, ... in the top left corner.

How many different squares can you make?
What is the largest square you can make?
Change the side total to 13, 17, 18, ...

You can only use each digit once (or not at all) for each total.
1 + 4 = 5 2 + 3 = 5 2 + 3 + 4 = 9
Investigate the different ways in which you can make all of the totals.
Keep a record of the different ways in which each total can be made.
Be systematic, looking for patterns in the totals.
What if taking away was allowed?

- Add sets of consecutive numbers.
- Write down the totals.
- Can you make every total up to 30?
- Which totals have the longest sets of consecutive numbers?
Try sets of two numbers, then sets of three numbers and so on.
What number patterns do you notice?
Make other totals up to 100. Are there any totals that you cannot make?

Explore solutions for this addition wall.

If you write a number that is a multiple of 2, score 2 points.
If you write a number that is a multiple of 3, score 3 points.
If you write a number that is a multiple of 4, score 4 points.
... and so on.
What is the best score you can make by totalling all the bricks you add to the wall?
What if the wall has four rows of bricks?
Why not choose your own total for the top brick?
Change the rule so that you find the difference between adjacent bricks.

After four rolls each of the dice you will have a pair of two-digit numbers.
Work out the difference between the two numbers.
Use the score chart to work out your score and find out who has won.

If the smallest difference is also odd, it scores 7 points!
Play your own version with a different score chart.

The total in each direction is the 'magic triple total' number.
What is the 'magic triple total' number for this grid?
Make up other 'magic triple total' grids with the same total as this grid.
Make up other grids with different 'magic triple totals'.
What is special about these totals?