Within the National Curriculum PoS, algebra only comes in as a discrete topic in Year 6:
Pupils should be taught to:
- use simple formulae
- generate and describe linear number sequences
- express missing number problems algebraically
- find pairs of numbers that satisfy an equation with two unknowns
- enumerate possibilities of combinations of two variables.
This use of algebra to represent numbers, make generalisations and solve problems obviously doesn’t just start in Year 6. It needs careful planning in each year so that children feel comfortable with using missing numbers, exploring patterns, using letters as unknowns and making general statements by the time they enter their final year of primary school.
Here are my top ten tips for making sure that algebra and pre-algebra is taught with confidence and also enjoyed by children:
-
Make the exploration of pattern the cornerstone of each maths topic – not just number patterns, but also patterns in calculations, shape properties, equivalent fractions… in fact all topics so that the children are always looking for general rules.
-
Ask the question, “What do you notice?” when looking at patterns so children never feel the pressure of a right or wrong answer and often make generalised statements without realizing.
-
Sort objects by use, size, colour, shape property, number property etc. to encourage children to look for general rules for sorting. Use Venn, Carroll and tree diagrams for sorting, increasing the number of criteria for sorting as the children progress through the school.
-
Play hiding games with cubes, counters or Compare-bears. Count out 7 cubes, hide 3 of them under a yoghurt pot and ask the children to work out how many are hidden. Record as __ + 4 = 7
-
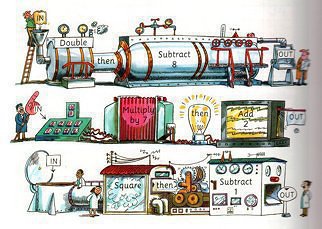
Make a large function machine out of a washing machine box (or something similar). Make an IN and an OUT door for children to go in and out and put a rule, such as +3 inside the box. They go in with a number on a card and write the answer on another card to blu-tac on to a table of results. Reinforce inverse operations by going backwards through the machine.
-
Use matchsticks and counters to generate sequences. Encourage children to describe any patterns they notice and to look for any relationships between the sticks and counters as the sequence develops.
-
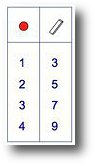
When looking at number patterns or functions, encourage children to always record the results in a table. Patterns are easier to see and the all-important function or rule is easier to work out and test.
-
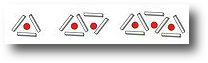
Instead of using x and y or other letters in equations, start with a box and triangle. y = x + 3 will make more sense of they have used
 = ∆ + 3 beforehand. The advantage is they can try writing different numbers in the triangle to work out the numbers represented by the square.
= ∆ + 3 beforehand. The advantage is they can try writing different numbers in the triangle to work out the numbers represented by the square.
-
Play ‘think of a number’ games and make sure they understand the importance of the inverse operation to solve them: I’m thinking of a number. I multiply it by 5, then take away 3. My answer is 22. What number did I start with? Relate this to going backwards through a function machine.
-
Use ‘think of a number’ sentences to teach substituting a letter for an unknown. For the example above, let the start number be y. The equation is then 5y - 3 = 22. They then solve it using the same process as ‘think of a number’ and going backwards through a function machine.