So what do children specifically need to know about place value? The following elements are all inter-related and are learnt together as a child makes sense of numbers, but these elements are worth considering separately. If a child is struggling with place value it is likely to be a misconception or error in one of these.
Base-10 structure
Our Hindu-Arabic system uses symbols for the numbers 1 to 9 and then a place value system with a place holder of 0. Using these ten symbols we are able to represent large numbers just by their value in different positions. Simple and efficient to us as adults – if you want to see what it is like for children to understand, try counting or calculating in base-5…! Teaching how our numbers go from 9 to 10 is almost impossible without the use of models to represent them.
The digits 1-9
Counting to 10 and getting to know the value of each of the numbers is the first step to getting a feel for larger numbers. If a child is having problems with sequencing or recognition it is often a skills issue related to the incorrect or inaccurate recital of counting words. Young children could have an unstable knowledge of numbers to 10 (Broadbent Maths users - read Early Counting Experiences). If this isn’t addressed then recognizing the value of these in larger numbers makes comparing and ordering of numbers an issue for some children.
Zero
Children need to recognize 0 as a label for an empty set, or nothing, as well as a place holder for numbers in our base-10 structure. It is the latter that is obviously the more difficult to understand, and it makes the use of structured apparatus to represent numbers so important. It becomes a particular issue when multiplying by 10 or 100, with zeroes magically ‘added’ to a number. This needs breaking down and modeling with 2-digit numbers and apparatus so they can see the effect on each digit when numbers are 10 or 100 times bigger.
Position of digits
The place or position of a digit in a number shows the value it represents, which, once understood, makes base-10 so much better than, say, base-2 for reading large numbers. This can still be tricky though, so highlighting every third digit back from the ones is helpful when distinguishing the number of hundreds, thousands and millions:
349 is 3 hundred and 49,
128349 is 128 thousand 3 hundred and 49
2128349 is 2 million, 128 thousand, 3 hundred and 49.
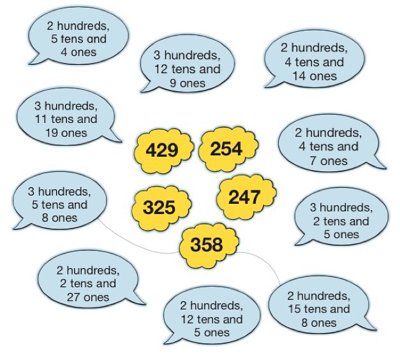
Partitioning
Using a developing understanding of the base-10 structure, partitioning involves separating out numbers so that the value of each digit can be seen, for example, 385 = 300 + 80 + 5. Confidence in doing this will be a pre-requisite to adding and subtracting larger numbers mentally and when using a written method. A step on is to partition in different ways, so 385 can also be shown as 300+70+15. This links well with exchange when learning to add and subtract.
It is worth pointing out the distinction that Thompson & Bramald (2002) make between quantity and column value of numbers.
Quantity value – being able to partition numbers e.g. 20 + 8
Column value – being able to say that 28 is 2 tens and 8 units
Quantity value is best used for the purposes of mental calculation, whereas column value is not needed until more formal written calculations are attempted.
Exchange
The principle of exchange is fundamental in mental and written calculations and is related to the value and position of each digit. Ten in any ‘place’ in a number can be exchanged for one in the next place to the left, so, for example, 10 hundreds can be exchanged for 1 thousand. Conversely, one in any ‘place’ can be exchanged for ten in the next place to the right, so for example, 1 hundred can be exchanged for 10 tens. The best way to understand this is to physically move base-10 material, exchanging 10 cubes for a 10-rod, for example.
Related article
Primary Maths activities for 2015
Use the digits 2, 0, 1 and 5 in a place value open ended task.
Progression steps - number
Use the small steps of progression for number during your Place Value teaching.
Models and images - place value
Use the PV arrow cards and number generator to represent numbers.