It is too easy to take our number system for granted, so try to teach it with a sense of awe and wonder. It is amazing to think that all our numbers are made with just nine digits and a zero (oh, and a decimal point...)!
When I started teaching we taught place value as a concept by using different base systems - so Base 5 was shown by bundling sticks in groups of 5 and also using 'multibase' equipment like the Dienes material. I'm not necessarily advocating it as a method, but it made us really consider the way our number system can be represented in different ways to help make sense of it all. Learning to count in base-2 is actually a great way to understand how you need another column or 'place' each time you have used up all the digits in one column.
What resources will support an understanding of place value?
Base 10 apparatus, such as Dienes, is still the most useful concrete representation of a number. The physical manipulation of each part of a number helps understand our number system. I find that using arrow cards alongside these at the same time gives a useful step towards the abstract, showing, for example, 482 as 400+80+2, or 480+2 or 400+82.
Place value counters are popular now and do a similar thing to arrow cards, bridging the gap between the base 10 apparatus and the actual numbers. They are particularly useful for showing exchange for calculations or on a place value mat.
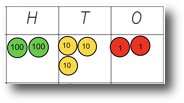
However, I still find I get more ‘Aha!’ moments with arrow cards if you want children to understand place value. Similarly, digit cards 0-9 used on a place value mat can be just as effective as PV counters. This is particulalry the case for making numbers 10 or 100 times larger or smaller.
An abacus isn’t used as much here as in many countries, but, again, it is a good step into the abstract, with each digit value represented by a bead. It certainly gives children a feel of the columns for hundreds, tens and ones. There are many types and the Japanese abacus, or soroban, is certainly worth using for children to explore numbers and ways of calculating with large numbers.

Also, don't always take the order of CPA literally to embed a child's understanding. Starting from the 'Abstract' often needs something 'Concrete' or 'Pictorial' for a demonstration of understanding. For example, ask a child to explain how adding 1 to 99 makes the number 100 - certainly an abstract concept. The explanation and demonstration using concrete models should show a real understanding (or not) of place value.
Understanding place value - 6 key aspects
What elements do children need to know?
Make your own interactive maths kit
There are some resources that could also be used for place value in this kit
Progression steps - number
The small steps of progression for number are useful for teaching Place Value
Models and Images - Place Value
Download, print and use the PV arrow cards and a number generator






