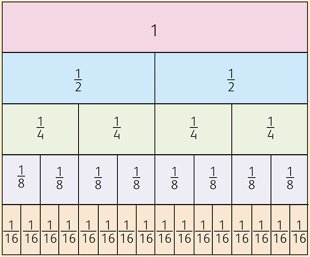
The language you use is important when showing the parts of a fraction.
In my Collins Maths Dictionary I explain it as follows:
 
The denominator shows you the number of equal parts that a whole shape or number is divided into. The numerator tells you how many of these equal parts you are using.
 
This can then be modelled using cubes or rods and shown as a diagram while using the language, then repeated for different fractions of a whole shape. It is important to keep the whole shape the same so that the equal parts of each can be compared.

Once children have a good feel for the meaning and purpose of each part of a fraction they should find it easier to understand the relationship between the numerator and denominator. 
 
The equivalence of fractional parts, eg 1/2, 2/4, 5/10 is seen clearly in measuring activities. If children find those fractions of 1 litre or 400 grams or 2 metres they will discover that for each of them the quantity is the same. They will be able to partition the whole into parts to work these out.
 
However, look out for children that are only ‘Part-Whole’ thinkers when they see fractions. They are likely to only operate with fractions by partitioning a quantity, measure or shape into equal-sized parts. The problem with this is they may struggle to understand fractions that are greater than one and will certainly have difficulties with ordering fractions and equivalent fractions.

Two fractions are equivalent when the numerator and denominator of one fraction are the same multiples of the numerator and denominator of the other fraction. To understand this you need to emphasise the ‘Part-to-Part’ relationship when comparing fractions. So when comparing 3/4 to 6/8 for example, you need to look at the relationship between the two numerators and the two denominators. Both have been multiplied by 2 so they are equivalent fractions.

Proportionality is a big idea in mathematics and a common error is for children to use addition or find the difference rather than multiply. This is why all the early counting work on patterns of multiples is very helpful so that the relationships leap out at the children. When they are written as a set of equivalent fractions in order, the patterns are even more striking:



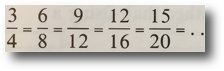
These can be represented on a number line, all sharing the same position.

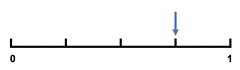
Children can draw in the smaller marked positions between each quarter for each equivalent fraction and look for patterns.





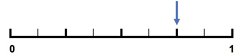
These set of equivalences can also be written as:

So the numerator and denominator have both been multiplied by 2, then 3, 4, 5... and so on.


Given plenty of opportunities to explore equivalent fractions, children will come to understand that there are an infinite number of equivalent fractions, but the ratio between the numerator and denominator always stays the same.