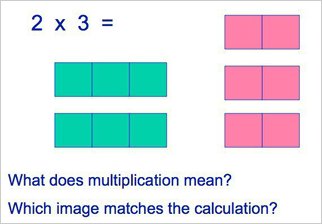
It really is all about how you interpret that x sign. If it is ‘groups of’ or ‘sets of’, then 2 groups of 3 is 3+3. If you see that sign as ‘multiplied by’, linking it to multiplication as scaling, then it is 2 multiplied by 3, or 2+2+2. This is obviously important at the early conceptual stage where a child is trying to visualize the maths going on and then also relating it to the language. Consistency with the language to match the action is important – are you emphasizing grouping and repeated addition or scaling and making an amount ‘three times larger’?
It is the way it is modeled and represented that can cause problems if it doesn’t match the language (or expected outcome), as illustrated in the recent marking controversy in the US:
Answers for 5x3 and 4x6 were marked as incorrect because of the way the child had interpreted the sign. Amazingly, it was even marked as incorrect for the very accurate array.
It is this second question marked as incorrect that is baffling because the array is the best way to illustrate that, say, 3x4 = 4x3. The commutative property of multiplication that makes this true and an array models it perfectly. It does not matter which way an array is drawn, it still shows four 3s or three 4s. The columns and rows can be grouped either way at this stage in a child’s understanding of the mathematics – it becomes important with matrices later in schooling, but this is a long way down the line.
What is good is the way they show the commutative value at the same time, so even if it is not how you would perhaps visualize the problem, the answer is clear and linked: five 4s and four 5s both give the answer of 20.
I still feel that repeated addition can be a limiting representation and using arrays is a better model, so link repeated addition to this when exploring multiplication. It is interesting to ask children what they see for 3x4 and how they would arrange cubes or counters in an array to show it. Ask them to talk it through and you’ll get a good idea of how they make sense of multiplication for themselves.
So what about our multiplication 'tables'? Is it the tables for 6x or is it the x6 tables?
The primary strategy recommended and encouraged the use of ‘multiplied by’ with the number of the table to learn first followed by the number it is being multiplied by – so 6x1, 6x2, 6x3, 6x4 etc. However, we now have the Shanghai and Singapore influence which will have an impact in our schools, and their model is consistently ‘groups of’, so 1x6, 2x6, 3x6, 4x6 etc. Which do I prefer? Oddly I haven’t really a preference – at the stage that children are learning facts then they should understand commutativity and say them both ways round. It doesn’t help that ‘times’ is vague and could mean ‘groups of’ or ‘multiplied by’. As a list on the wall it is easy to see the ‘tables’ you are practicing if it comes first (as they have in Switzerland). However, when practicing them orally with a class, we tend to chant ‘one 3 is 3, two 3s are 6, three 3s are 9, four 3s are 12… so it may help children to read it in the same order, 1x3, 2x3, 3x3, 4x3…