Looking at maths in nature should certainly inspire children... and teachers. Counting spirals on cones and sunflowers can reveal Fibonacci numbers. Children can discover the rules behind these special numbers and use the numbers to draw spirals that look like shells – which takes them back to nature again!
Back in April I wrote an article, Growing plants and maths activities and I suggested you grow some sunflowers. These should be ready now. Sunflowers and cones are the easiest spirals to count and should give you the Fibonacci numbers 5, 8, 13, 21, 34, 55 and so on.
And ask some questions.
Inspire your class
Show some pictures of spirals in nature. Explain that if you counted the spirals on plants you always come up with the same set of numbers.And ask some questions.
Get involved with the Turing experiment and submit your data to the sunflowers experiment. You need to count sunflower seeds rather than the flowers and measure the diameter (more maths!) so there is a bit more detail needed but it gives a real purpose to the task. There are instructions on how to measure and join in.
How to count the spirals
A pineapple is good to demonstrate with. Use strips of coloured sticky tape to mark each spiral in one direction, counting as you go and then in the other direction.The easiest way to count spirals on a cone is to use coloured pens and follow the spiral, they are often easier to see on the side the cone. Count as you colour each one - if you look from the base you will see spirals one way and if you look from the top you will see different spirals (these were not clear on my cones though). Children will discover that the number of spirals in this direction is different. You can see the spiral on some closed cones immediately, however some will grow unevenly so put those to one side. Open cones are very difficult to count.
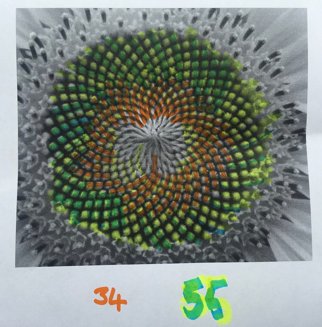
With sunflowers it is much easier to count on paper. Children can photograph their sunflowers and print them, like the examples shown above and here. Colour the spirals in both directions as you count.
The sunflower above has 34 spirals in one direction and 55 spirals in the other direction. The one at the side again has 55 spirals. Yes – Fibonacci numbers again.
Search cacti spirals images you will get a screen of easy to count spirals, children can count on screen using the cursor to remind them of their starting point. Some spirals that wrap round a long way are easier to count near the centre, while those with a larger number of spirals are easier to count a little further out as the spirals are too tightly packed at the centre.
The sunflower above has 34 spirals in one direction and 55 spirals in the other direction. The one at the side again has 55 spirals. Yes – Fibonacci numbers again.
Search cacti spirals images you will get a screen of easy to count spirals, children can count on screen using the cursor to remind them of their starting point. Some spirals that wrap round a long way are easier to count near the centre, while those with a larger number of spirals are easier to count a little further out as the spirals are too tightly packed at the centre.
What are the numbers you’ve found?
• Write everyone’s numbers on the board, grouping together or keeping a tally of each number. Then get the children to place the numbers in order.
• What do you notice about the numbers? Is there a pattern?
• Talk about the things they looked for or could look for, such as multiples, looking at the numbers on a number line or finding the difference.
• Can they predict the next number?
• Can they find the number before 5? And earlier numbers?
Numbers in the sequence are made from the sum of the previous two numbers, 8 + 13 is 21
These are Fibonacci numbers. 1 1 2 3 5 8 13 21 34 55
What can we do with these numbers?
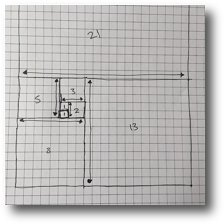
Draw them as joining squares:
1 x1 square, next to a 1x1 square,
2 x 2 square, along the side of the two 1s squares,
3 x 3 square along the side of a 1 and 2 square
continue with 5 x 5, 8 x 8, 13 x 13 and 21 x 21 squares.
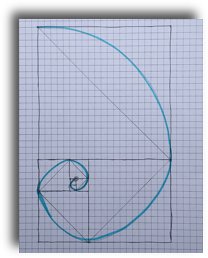
This is a great pattern in itself, but add some diagonal curves and from Fibonnaci numbers you can then create spirals, like those in nature.
Start on a corner of a 1x1 square that joins the 2 x 2 square. Draw diagonal lines across the corners of each square following on from the last one – so there is one complete line.
If a curved line is drawn free-hand around these straight diagonal lines you get a spiral that looks like a nautilus shell – and back to nature from the numbers.
If a curved line is drawn free-hand around these straight diagonal lines you get a spiral that looks like a nautilus shell – and back to nature from the numbers.
Highly recommended Youtube clip from Vi Hart about Fibonacci numbers and spirals.
This will inspire you so watch it now - and enjoy.
For your class I suggest watching it after they have completed some of the work. It will reinforce the number pattern and how they are linked to spirals in nature.
In addition there are a number of suggestions to investigate Fibonacci numbers further, this could be an extension activity for those that have finished early.
Related articles
Fibonacci maths activity
Number sequence activities
Growing plants and maths activities
Learn maths while you watch your sunflowers grow
Fibonacci maths activity
Number sequence activities
Growing plants and maths activities
Learn maths while you watch your sunflowers grow