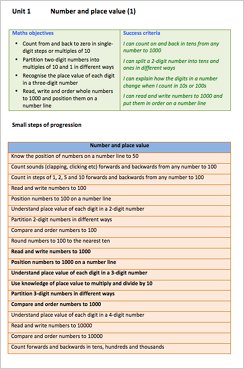
When planning a unit of maths, the learning objectives are a key starting point. All teachers begin with a set of objectives, with many teachers then using success criteria as expected outcomes. I also like to use small steps of progression alongside these.
I think it is worthwhile looking at the purpose of each of them, to make the most of these linked aspects at the start of the planning process.
The maths objectives are the curriculum goals for a unit of work: what the pupils will know, understand or be able to do by the end of the unit.
They outline how the National Curriculum programmes of study have been broken down and then sequenced to make sure there is coverage, progression and continuity. They can be relatively broad in scope and some are very similar when repeated again later in the year, with the detail of the success criteria showing the specific change in emphasis. The objectives are for you to use as a reference so that you can have a clear unit focus and so that you can identify more specific lesson objectives when planning a sequence of lessons.
The success criteria statements are formed out of these objectives, giving a clear idea of the evidence you will be looking for to identify whether your pupils have met the learning objectives.
They should be in child-friendly terms as the pupils themselves should be part of the process of assessing whether they have made progress and been successful in meeting the objectives. They also identify specific aspects to focus on from the objectives.
For example, look at this objective for a Year 4 Shape and Symmetry unit:
This gives the curriculum focus and goal, but it is the success criteria that helps pin-point the evidence you will be looking for when they classify shapes:
So, what about the small steps of progression? These are closely linked to the objectives, but help you to fine-tune your teaching, breaking down the objectives into separate steps.
These steps show the development of a particular strand of maths, giving you a clear ‘journey’ of the early concepts or skills a child will experience, through to the more advanced expectations by the end of Y6. It aims to help with differentiation – find out where the majority of your class are pitched (in bold on the template) and then look at the previous steps for your lower attainers and the next steps for your high attaining group. Pupils are not expected to cover all the small steps in a unit, it simply identifies the steps they are likely to take, which could be just one or two in a 2-week unit. Also, maths learning is not linear – there are lots of inter-connections, so it may be that there will be steps they show good understanding of, with some gaps evident in their previous steps.
These small steps of progression are particularly effective if shared with the pupils as part of their formative assessment. They can then be ‘owners of their own learning’ as Dylan Wiliam put it – knowing the next steps to aim for or to identify any gaps in their knowledge and understanding. Schools have successfully used them as a reference sheet of steps for the pupils to have in their books at the start of a new unit, using smiley faces or a scale to record progress.
Hope this helps you pick through the differences and links between each of these. There is no doubt that identifying the learning objectives, developing the expected outcomes as success criteria and understanding the progression inherent in each maths topic is an essential part of your planning and an important feature of your ‘deep’ subject knowledge.